David silver’s reinforcement learning lecture 2

2 minute read

Markov Decision Processes

※ RL 문제의 대부분은 MDP로 변환시켜 적용할 수 있음

1. Markov Property

현재 t에서의 state가 이전의 모든 정보(history)를 포함하고 있어서 미래를 고려할 때 현재의 state만 고려해도 된다.

2. State Transition Matrix

state transition probability

현재 state에서 다음 state가 될 확률.
state transition matrix

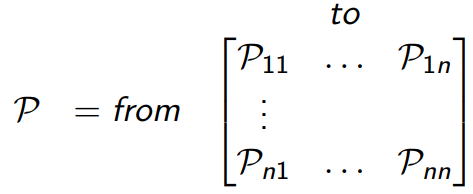
n개의 state를 고려하면 matrix가 된다. 즉, P1n은 1-state에서 n-state로 갈 확률.

각 row의 합은 1이 된다.

3. Markov Process

Markov Process는 state들의 집합인 S와 state transition probability matrix들의 집합인 P만 있는 것.

여기서 memoryless가 의미하는 것은 이전 정보가 필요 없다는 것. 즉, markov property를 만족한다는 것.

example

여기서 sleep이 terminal state(episode가 종료되는 state)

4. Markov Reward Process

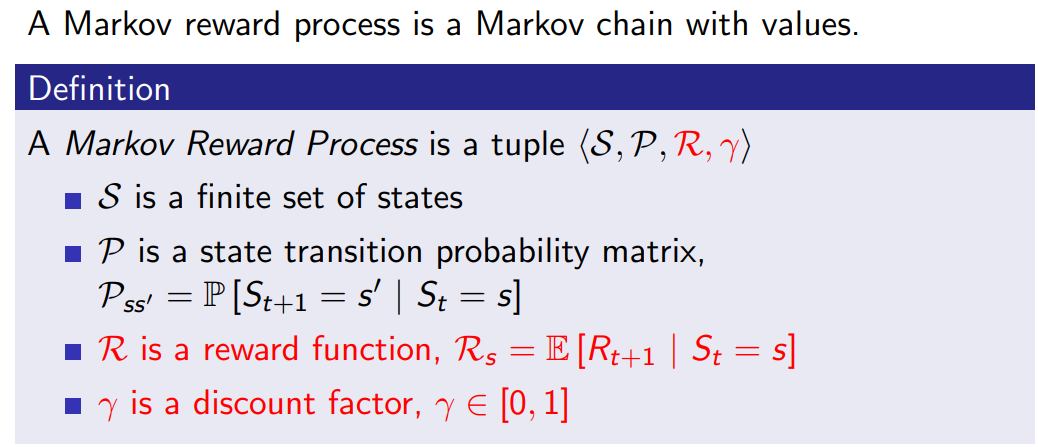
Markov Reward Process는 markov process에서 reward가 추가된 것.

Return

Return은 미래에 축적될 reward들을 다 더한 값. 즉, return을 최대화 시키는 것이 목적이다.

discount가 0에 가까우면 현재의 reward가 중요하게 되고, 1에 가까우면 미래의 reward가 중요하게 된다.
Value Function

markov reward process에서 value function은 return의 기댓값이다.
Bellman Equation for MRPs

바로 다음 state의 value function을 통해 값을 구한다.

이것을 간단하게 표현하면 아래와 같다.

여기서 v를 바로 구할 수 있다. 왜냐하면 MRP에서는 discount, R, P가 주어지는 문제이기 때문에.

5. Markov Decision Process

MDP는 MRP에서 action의 집합이 추가된다.

policy

policy는 현재 state에 의존(history가 아니라). 즉, stationary(time-independent)하다.

일정 확률로 action을 취했을 때, 각 action마다 다음 state로 넘어가는 확률이 또 다르기 때문에 변수가 많아짐.

MDP에서 P와 R을 위와 같이 계산을 하여 고정시키면 결국 MP나 MRP 문제가 된다고 볼 수 있다.
Value Function

action-value function은 q-function이라고도 한다. Q-learning과 DQN에서의 Q가 이 action-value function을 의미.
Bellman Expectation Equation

MRP에서의 벨만방정식의 논리와 같다.

q는 v에서 해당 state에서 취할 수 있는 action까지 고려한, 더 세분화한 함수라고 보면 된다.

두 식의 관계는 위와 같다. 현재 state에서 취할 수 있는 action들을 다 고려해서 더하면 결국 v가 된다.

반대로 q는 현재의 reward에다가 어떤 action을 취했을 때 나올 수 있는 state들의 v를 더하면 된다.

식들을 서로에게 대입하면 위의 식처럼 나온다.

결국 이처럼 direct solution을 도출할 수 있다.
Optimal Value Function

최대값을 갖는 것이 곧 최적의 값이다. 즉, MDP를 풀었다고 할 수 있다.
Optimal Policy

policy는 모든 state에 대해서 한 policy에 따른 v가 다른 policy에 따른 v보다 항상 크거나 같아야 더 좋다고 할 수 있다.

또한, 최적의 policy에 따라 v, q를 구하면 그것이 최적이 된다.

반대로 최적의 q를 따라가면 최적의 policy를 찾을 수 있다.

신기하게도 MDP에서는 확률적이지 않은, 즉 deteministic한 최적의 policy가 존재한다.
Bellman optimality equations

최적의 q에서 최대의 값을 갖게 하는 a를 따라가면 그게 최적의 v이다.

Bellman expectation equations와 달리 bellman optimality equations는 행렬 계산으로 풀 수가 없다.(No closed form)

즉, non-linear하다.

이것을 풀기 위한 방법들은 다음과 같다.
- Value Iteration
- Policy Iteration
- Q-learning
- Sarsa