David silver’s reinforcement learning lecture 3

Planning by Dynamic Programming

​ ※ planning은 MDP에 대한 모든 지식(model, environment 등)을 알고 있을 때 최적의 value function을 찾는 문제

1. Requirements for Dynamic Programming

Dynamic Programming을 사용하기 위해선 두 가지 조건을 만족해야 한다.

• Optimal substructure : optimal solution이 subproblem으로 쪼개질 수 있어야 한다.
• Overlapping subproblems : subproblems의 solution이 여러번 다시 사용될 수 있어야 한다.

MDP는 이 조건들을 만족하기 때문에 DP를 사용할 수 있다.

2. Policy Evaluation

Policy Evaluation은 policy가 주어졌을 때 value function을 구해서 평가하는 prediction 문제이다.

• Iterative Policy Evaluation

  

  policy와 reward가 주어졌을 때, Bellman Equation을 가지고 매 iteration마다 value function을 조금씩 개선한다.

  
  

• Example : Small Gridworld

  

  위와 같은 예시로 policy iteration을 진행해보자.

  ​
  

  

  

  여기서 3번만 반복해도(valuation이 최적화 되지 않아도) optimal policy가 나온 것을 확인할 수 있다.

  평가하는 문제에서 최적의 policy를 찾을 수 있다는 것을 보여준다.

  
  

3. Policy Iteration

Policy Evaluation에서 policy improvement 를 추가한 것이 policy iteration이다.

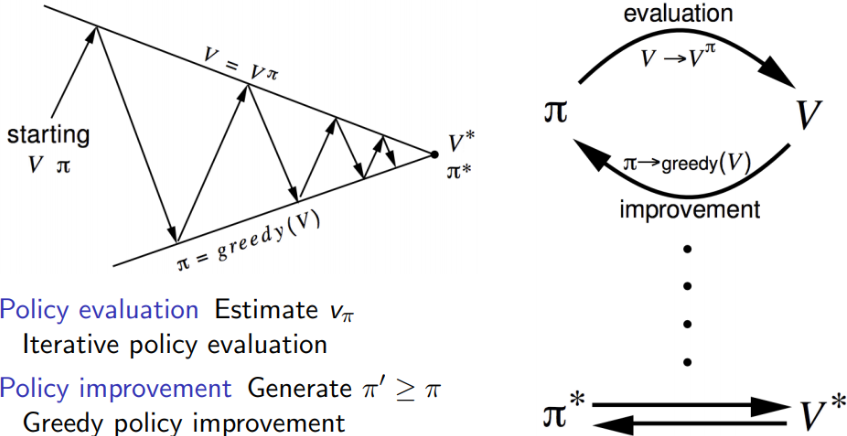
evaluation을 통해 개선된 value function을 기반으로 policy를 개선. 반복하면 결국 최적으로 수렴한다.

• Policy Improvement

  그럼 정말로 처음에 좋지 않던 value function을 기반으로 policy를 개선해 나가는데, 이것이 최적으로 수렴이 되나?

  이 질문에 대한 증명이 아래와 같다.

  

  이 수식은 어떻게 보면 당연하다. action-value function(q-function)의 최댓값을 내는 action을 따르면 당연히 그 어떤 action들에 의해서 나오는 값보다는 크거나 같기 때문이다.

  
  

  세 번째 식의 의미를 정리해보면,

  

  A : 첫 action만 새로운 policy에 따라 행동하고 그 다음부턴 기존의 policy에 따른 q

  B : 처음부터 끝까지 기존의 policy에 따른 q

  A가 B보다 당연히 크거나 같은 이유는 새로운 policy는 최댓값을 갖는 action을 뽑아냈기 때문이다.

  
  

  마지막 수식들은 세 번째 식과 Bellman equation을 반복해서 적용한 것이다.

  
  

  

  결국, 최적의 policy와 value function을 찾을 수 있다.

  
  

  여기서 몇 가지 질문들을 할 수 있다.

  • value function은 더 좋아질 수 있는데 꼭 최적의 policy를 찾았을 때를 기준으로 해야 하는가?
  • 꼭 매 iteration 마다 policy를 업데이트 해야하나? 3번 evaluation하고 업데이트 하는 방식은 안되나?

  
  

4. Value Iteration

value iteration은 뒤에서부터 차례로 최적의 optimal solution을 찾으면서 update를 해나간다.

이렇게 얻은 optimal v로부터 optimal policy를 찾는 것이다.

즉, 아래의 식을 뒤에서부터(terminal state에서부터) 반복 계산하면서 optimal solution을 찾는다.

• Summary of DP Algorithms

  

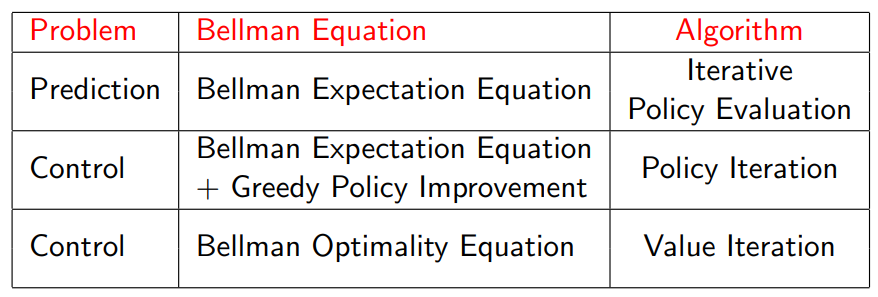
5. Asynchronous Dynamic Programming

지금까지 배운 DP는 synchronous DP 였다. 즉, 각 state에서의 값들이 한 번에 병렬적으로 처리되면서 update된다.

하지만 synchronous 방법은 계산량이 너무 많다는 단점이 있다. 이것을 보완하는 방법이 asynchronous DP이다.

Asynchronous DP의 장점

• state들을 개별적으로 back up하고 계산하기 때문에 연산량을 줄일 수 있다.
• 만약 모든 state들이 계속해서 선택된다는 보장만 있다면, synchronous와 같이 최적으로 수렴할 수 있다.

Asynchronous DP의 3가지 간단한 방법

• In-Place Dynamic Programming

  

  이 방법은 프로그래밍 skill이다. n개의 state가 있는 MDP의 경우, policy iteration, value iteration을 코딩한다면 원래는 이전 정보를 담은 table과 새로 업데이트 할 table 두 개가 필요하다.

  하지만, 이 방법은 그냥 하나의 table만 쓰고 어떤 state의 정보를 update할 때 table 내에서 방금 update 된 이전 state들의 정보를 가져다 쓰자는 것이다.

  
  

• Prioritised Sweeping

  

  state를 업데이트 하는 순서는 상관이 없기 때문에, 우선순위가 높은 것들을 먼저 update하는 방법이다.

  이때, 우선순위를 파악하는 방법은 Bellman error이다.

  Bellman error가 큰 것들이 우선순위가 높은 것이다. 여기서 bellman error는 이전 정보(table)와 현재 정보(table)를 비교했을 때 차이가 큰 것이 우선순위가 높은 것.

  
  

• Real-Time Dynamic Programming

  

  agent가 state space를 돌아다니면서 방문한 state들을 먼저 update하는 방법이다.

6. Backup method

• Full-width Backups

  지금까지 우리는 한 state에서 갈 수 있는 모든 state들을 고려하여 backup을 했다.

  이 방법의 문제점은 large scale일 경우에 너무 비효율적이고 연산량이 급격하게 많아진다는 것(차원의 저주)이다.

  즉, one backup can be too expensive 하다는 문제가 있다.

• Sample Backups

  이 방법은 full-width backups 방법을 보완한 것이다.

  한 state에서 나올 수 있는 모든 successor state에 대해서 하는 것이 아니라 지정한 sample의 갯수만큼의 successor state에 대해서 backup을 하는 방식이다.

  Advantages :

  • Model-free : agent의 action에 따른 다음 state들을 얻을 수 있으므로 n번의 action을 해서 나온 state들에 대해서 backup을 한다면 model-based가 아니어도 적용할 수 있다.
  • 차원의 저주를 해결할 수 있다.

​

※ 참고문헌 및 자료

• [David Silver’s Lecture]
• [팡요랩]