David silver’s reinforcement learning lecture 5

Model-Free Control

1. On and Off-Policy Learning

• On-policy learning

  현재 움직이고 있는(action을 취하는) policy와 improve하는 policy가 같다.

  
  

• Off-policy learning

  action을 취하는 policy(behavior policy)와 improve하는 policy(target policy)를 다르게 취한다.

  
  

2. On-policy Monte-Carlo Control

Policy Iteration을 다시 보면, policy evaluation과 policy improvement를 반복해서 최적의 policy를 찾아낸다(단, model-baesd인 상황에서).

그렇다면 policy evaluation을 mc를 적용하고 policy improvement를 기존처럼 greedy policy improvement를 사용하면 model-free에서 control 문제를 풀 수 있지 않을까 생각할 수 있다. 하지만, 기존의 greedy policy improvement는 MDP를 알아야(model-based)하므로 불가능하다.

value function은 MDP model을 알아야 greedy policy improvement가 가능(기존 방식).

그치만 q-function은 model-free에 대해서도 greedy policy improvement가 가능하다. model은 몰라도 action을 해보고 거기서 나오는 state 중에서 최댓값을 얻을 수 있으니까.

위의 예시는 action-value function기반의 MC로 policy iteration을 풀 때의 문제점을 보여준다.

처음에 오른쪽 문을 열었을 때가 reward를 주기 때문에 agent는 계속해서 오른쪽이 더 좋은줄 알고 오른쪽만 연다.

처음 단 한번의 선택으로 이것이 최적으로 향하는 것일까? 그렇지 않다는 것이다. 모든 state들에 대해서 고려하지 않을 수 있기 때문이다.

이 문제를 보완한 것이 ε-greedy exploration이다.

• ε-Greedy Exploration

  

  낮은 확률(ε/m)로 임의의 다른 action을 취하도록 함으로써 모든 state들을 고려할 수 있게 하고, 높은 확률로 최대의 q function을 갖도록 하는 action을 함으로써 최적으로 수렴하게 한다.

  
  

  

  ε-greedy exploration을 쓰면 왜 최적으로 수혐하는지, 왜 개선이 되는지를 수식으로 나타낸 것이다.

• Monte-Carlo Policy Iteration

  

  정리하면 다음과 같이 policy evaluation은 MC, policy improvement는 ε-greedy policy improvement를 사용.

• Monte-Carlo Control

  

  좀 더 효율적으로 하기 위해서 sampling한 episode들 전체가 끝날 때까지 기다리는 게 아니라, 매 episode가 끝날 때마다 평가하고 개선하는 방법이다.

  
  

  • Greedy in the Limit with Infinite Exploration (GLIE)

    

    GLIE는 두 가지 조건을 의미한다.

    첫 번째로, atate-action 쌍이 무한히 많이 탐험되어야 한다는 것.

    두 번째로, policy가 greedy policy 즉, optimal policy로 수렴해야 한다는 것.

    하지만 epsilon greedy는 greedy하게 하나의 action만 선택하지 않는데 이럴 경우는 GLIE하지않다.

    그치만 만약 epsilon이 시간에 따라서 0으로 수렴(1/k)한다면 epsilon greedy 또한 GLIE가 될 수 있다.

    
    

    • GLIE Monte-Carlo Contorl

      

      이렇게 GLIE MC control이 완성된다.

      
      

  ## 3. On-policy Temporal-Difference Learning

  이제는 TD를 이용한 policy control 문제를 다룬다.

  
  

  • Sarsa

    

    그림과 같이 현재의 State에서 Action을 취했을 때 얻는 Reward, 그리고 다음 State에서 취할 Action을 고려하는 게 한 step이고 매 step마다 update가 된다. TD(0)에서 state-value function 대신 action-value function을 사용한다.

    
    

    

    TD이기 때문에 매 step마다 update가 되는 것이고, 이때 policy evaluation으로 Sarsa를 사용한다.

    
    

    

    Sarsa의 algorithm을 보면 위와 같다. on-policy TD control algorithm으로서 매 time-step마다 현재의 Q value를 imediate reward와 다음 action의 Q value를 가지고 update한다. policy는 따로 정의되지는 않고 이 Q value를 보고 epsilon-greedy하게 움직이는 것 자체가 policy이다.

    
    

    

    Sarsa는 optimal action-value function에 수렴한다. 단, 조건이 있다.

    위에서 언급한 GLIE를 만족해야 한다.

    step-size(얼마나 update할 지 정하는 매개변수)도 위와 같은 조건을 만족해야 한다.

    • q value가 매우 큰 경우를 위해서 이 값에 도달하기 위해 step size가 어느 정도 커야 한다.
    • 뒤로 갈수록(시간이 지날수록) update 정도가 줄어들어야 한다. 즉, 수렴이 되어야 한다.

    
    

    • n-Step Sarsa

      

      n-step TD랑 똑같지만 return 대신 Q-function이 사용되었다.

      
      

    • Forward View Sarsa(λ)

      

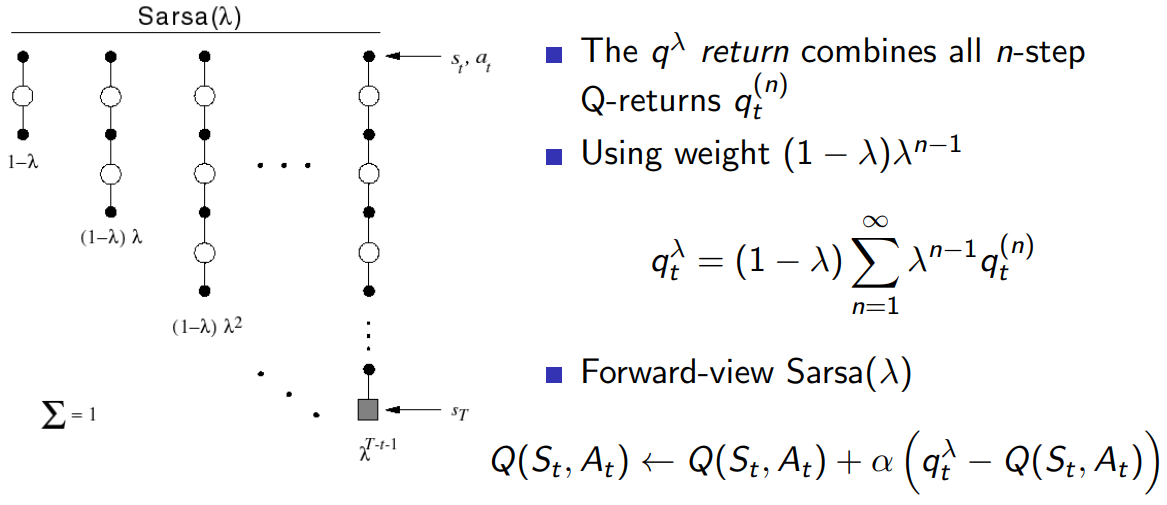
      forward도 마찬가지다.

      
      

    • Backward View Sarsa(λ)

      

      backward도 마찬가지로 return 대신 q-function을 사용.

      알고리즘은 아래와 같다.

      

      한 번의 action으로 모든 state와 action을 update 해준다. 연산량이 많지만, 정보 전달 속도가 빠르다. 이것은 아래의 예제에서 확인할 수 있다.

      

      one-step Sarsa는 목적지에 도착하면 바로 이전 state만 크게 update 되지만, Sarsa(λ)는 한참 전의 state들도 한 번에 update 되는 것을 알 수 있다. 이것은 eligibility trace 때문이라고 생각한다.

      
      

  ## 4. Off-Policy Learning

  

  on-policy는 한계가 있다. 바로 탐험의 문제다. 현재알고있는 정보에 대해 greedy로 policy를 정해버리면 optimal에 가지 못 할 확률이 커지기 때문에 에이전트는 항상 탐험이 필요하다. 따라서 on-policy처럼 움직이는 policy(behaviour policy)와 학습하는 policy(target policy)가 같은 것이 아니고 이 두개의 policy를 분리시킨 것이 off-policy이다.

  Off-policy는 다음과 같은 장점이 있다.

  • 다른 agent나 사람을 관찰하고 그로부터 학습할 수 있다
  • 이전의 policy들을 재활용하여 학습할 수 있다.
  • 탐험을 계속 하면서도 optimal한 policy를 학습할 수 있다.(Q-learning)
  • 하나의 policy를 따르면서 여러개의 policy를 학습할 수 있다.

  
  

  
  

  • Importance Sampling

    

    어떤 값을 추정하는데 가장 기본적인 방법은 그냥 random하게 찍어보는 것이다. 하지만 너무 광범위하게 탐색하기도 하고 어떠한 중요한 부분을 알아서 그 위주로 탐색을 하면 더 빠르고 효율적으로 값을 추정할 수 있고 그러한 아이디어가 바로 “Importance Sampling”이다.

    P와 q라는 다른 distribution이 있을 때 q라는 distribution에서 실재로 진행을 함에도 불구하고 p로 추정하는 것처럼 할 수 있다는 것이다. 강화학습에서도 policy가 다르면 state의 distribution은 달라지게 되어 있다. 따라서 다른 distribution을 통해 추정할 수 있다는 개념을 그대로 가져와서 다른 policy를 통해서 얻어진 sample을 이용하여 Q 값을 추정할 수 있다는 것이다. 일종의 trick이라고 할 수 있을 것 같다.

    f(X)라는 함수를 value function이라고 생각하고 강화학습에서는 이 value function = expected future reward를 계속 추정해나가는데 P(X)라는 현재 policy로 형성된 distribution으로부터 학습을 하고 있었습니다. 하지만 다른 Q라는 distribution을 따르면서도 똑같이 학습할 수 있는데 단, 위와 같이 간단히 식을 변형시켜주면 된다.

  
  

  • Importance Sampling for Off-Policy Monte-Carlo

    

    각 스텝에 reward를 받게 된 것은 μ-policy를 따라서 얻었던 것이므로 매 step마다 π/μ를 해줘야 한다.

    episode가 끝날 때까지 곱해주기 때문에 값이 매우 작아지거나 매우 커지게 되는 문제가 발생하기 때문에 Monte-Carlo에 off-policy를 적용시키는 것은 좋지 않다.

    
    

  • Importance Sampling for Off-Policy TD

    

    Off-Police TD에서는 MC 때와는 달리 Importance Sampling을 1-step만 진행하면 된다.

    MC때와 비교하면 Variance가 낮아지기는 했지만 여전히 원래 TD에 비하면 Importance sampling때문에 높은 variance를 가지고 있다는 문제점이 있다. 그래서 나오게 된 것이 Q Learning이다.

    
    

  • Q-Learning

    

    현재 state S에서 action을 선택하는 것은 behaviour policy를 따라서 선택을 한다. TD에서 udpate할 때는 one-step을 bootstrap하는데 이 때 다음 state의 action을 선택하는 데는 behaviour policy와는 다른 policy(alternative policy)를 사용하면 Importance Sampling이 필요하지 않다. 이전의 Off-Policy에서는 Value function을 사용했었는데 여기서는 action-value function을 사용함으로써 다음 action까지 선택을 해야하는데 그 때 다른 policy를 사용한다는 것이다.

    
    

  • Off-Policy Control with Q-Learning

    

    이 Q-learning 알고리즘이 가장 유명하고 많이 쓰인다.

    greedy한 policy로 학습을 진행하면 수렴을 빨리 하는데 충분히 탐험을 하지 않았기 때문에 local에 빠지기 쉽다. 그래서 탐험을 위해서 ε-greedy policy를 사용하면 탐험을 계속하는데 이렇게 학습하면 수렴속도가 느려져서 학습속도가 느려지게 된다. 그래서 target policy는 greedy로 빠르게 최적으로 향하게 한다.

    

    • Behaviour policy로는 g-greedy w.r.t. Q(s,a)

    • Target policy(alternative policy)로는 greedy w.r.t. Q(s,a)

    위와 같이 최적의 action-value function으로 수렴하게 된다.

    
    

    • Algorithm

      

      
      

  • Relationship Between DP and TD

    

※ 참고문헌 및 자료

• [David Silver’s Lecture]
• [팡요랩]
• [Fundamental of Reinforcement Learning]